|
|
Advektion
|
|
Defintion: Das negative Skalarprodukt aus Windvektor und dem Gradienten einer skalaren oder vektoriellen meteorologischen Größe wird als Advektion dieser Größe bezeichnet. Anschauung und Verwendung: Die Advektion ergibt sich in der Hydrodynamik bei der Betrachtung EULER´scher Luftpakete. Diese ortsfesten Luftpakete können ihre charakteristischen Größen zum einen lokalzeitlich, aber auch durch den Herantransport mit dem Wind ändern. Die Advektion beschreibt den Transport einer meteorologischen Größe in ein EULER´sches (ortsfestes) Luftpaket. Dabei ist die Advektion keine reine Transportgröße sondern per Definition auch vom Gradienten der betrachteten Größe und seiner Lage zum Windvektor abhängig. Stehen beide Vektoren senkrecht aufeinander, so verschwindet die Advektion. Das negative Vorzeichen ergibt sich aus anschaulichen Überlegungen. Hierzu soll folgende Skizze für die Temperaturadvektion hilfreich sein. 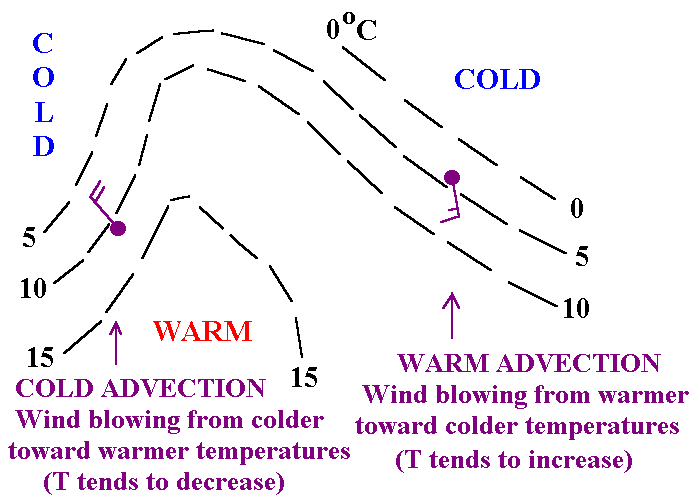 Auf der linken Seite zeigt der Temperaturgradient zur warmen Luft und ist dementsprechend genau gleichgerichtet mit dem Windvektor. Somit ergibt sich bei der Kaltluftadvektion auf der linken Seite ein positives Skalarprodukt. Umgekehrt sind auf der rechten Seite im Falle der Warmluftadvektion die beiden Vektoren genau entgegengerichtet, so dass hier ein negativer Wert für die TA herauskommt. Da WLA aber mit Temperaturerhöhung einhergeht, hat man sich darauf geeinigt auch eine positive TA zu definieren, so dass das eingangs in der Definition erwähnte Minuszeichen bei der Berechnung der Advektion nun seine anschauliche Berechtigung erfährt. Eine Besonderheit stellt die Advektion vektorieller Größen dar. Ergebnis einer solchen Berechnung ist dann keine skalare Größe mehr sondern ein (Advektions)vektor. © Marcus Boljahn |