Idee:

Damit ein Luftpaket ein gewisses Höhennivaeu erreichen kann, muss es eine entsprechende Arbeit gegen die Schwerkraft verrichten. Das Luftpaket erhält also potentielle Energie. Flächen gleicher potentieller Energie werden allgemein als Niveauflächen bezeichnet, wobei speziell auf die Erde bezogen der Begriff Geopotentialflächen eingeführt wurde.
Da die Schwerkraft durch die nicht ganz kugelmetrische Masseverteilung im Inneren unseres rotierenden Planeten inhomogen ist, verlaufen demnach auch die Geopotentialflächen ebenfalls nicht ganz parallel zur Meeresoberfläche. Daher wird bei meteorologischen Betrachtungen statt der geometrischen Höhe eher das Geopotential als Höhenkoordinate verwendet. Linien gleicher geopotentieller Höhe werden als Isohypsen bezeichnet.


Defintion:

Die Arbeit, die nötig ist, um ein Luftpaket (mit Einheitsmasse) vom Meeresspiegel (0) auf ein Niveau Z zu heben, wird als Geopotential bezeichnet.


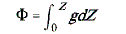
Da die Schwerebeschleunigung als nahezu höhenkonstant angesehen werden kann, reduziert sich das Geopotential auf das Produkt von Schwerebeschleunigung und geometrischer Höhe.


Anschauung:

Da die Schwerebeschleunigung am Äquator ihre niedrigsten Werte aufweist und die Höhe der Geopotentialflächen umgekehrt proportional zur Schwerebeschleunigung ist, liegen dort auch die Geopotentialflächen geringfügig höher als an den Polen.
Für die Praxis wird darüber hinaus das geopotentielle Meter (gpm) über die Wichtung mit der Schwerebschleunigung in 45° definiert, damit die Höhe der Isohypsen ungefähr der Höhe über dem Meeresspiegel entspricht.
1 gpm:=9,80665m²/s²

Anwendung:

Bei vielen meteorologischen Betrachtungen spielt die Dichte und deren Einfluss eine direkte Rolle. Nun erweist sich aber insbesondere die Messung der Luftdichte als sehr problematisch, vor allem bei Radiosondenaufstiegen, da die Dichte einer Temperatur- und Höhenabhängigkeit unterliegt.
Über die hydrostatische Grundgleichung gelingt es nun dieses scheinbare Dilemma zu umgehen, indem man hier nach dem Geopotential umstellt. Dadurch wird dann statt der Höhe Z der Druck p als Höhenkoordinate verwendet.
Mit Hilfe dieser einfachen äquivalenten Umformung lässt sich nun aus vielen Gleichungen im Z-System die Dichte eliminieren, einfach indem man den Druck als Höhenkoordinate benutzt (p-System). Bekanntestes Beispiel ist hier der geostrophische Wind, der im z-System durch den Dichteeinfluss nur quasiparallel zu den Isohypsen weht, während er im p-System dann exakt parallel zu den Isolinien des Geopotentials verläuft.

Im Theta-System reicht allein die Betrachtung des Geopotentials nicht mehr aus. Da die aus thermodynamischen Betrachtungen abgeleitete Größe der potentiellen Temperatur dort als Höhenkoordinate fungiert, kommt zum Geopotential noch die Enthalpie sozusagen als thermodynamisches Potential noch hinzu. Die Summe aus beidem wird nach ihrem Entdecker als MONTGOMERY-Potential bezeichnet.
Der geostrophische Wind im Theta-System verläuft dann natürlich wieder parallel zu den Linien gleichen MONTGOMERY-Potentials.

© Marcus Boljahn