Definition:

Ein Wind, der im Gleichgewicht zwischen Druckgradient- und Corioliskraft weht, wird als geostrophischer Wind bezeichnet. Geostrophisches Gleichgewicht oder Geostrophie sind die Bezeichnungen für dieses horizontale Gleichgewicht. Das der geostrophische Wind in der Natur eigentlich nie exakt so weht, spricht man auch von der geostrophischen Approximation. Abweichungen vom geostrophischen Wind werden ageostrophischer Wind genannt.


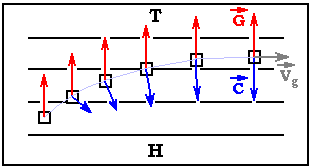
Quelle: www.wetter3.de

Ein zunächst nur durch die Druckgradientkraft (rote Pfeile) beschleunigtes Luftteilchen wird in Bewegung gesetzt und erfährt nun (auf der Nordhalbkugel) eine zunehmende Rechtsablenkung durch die Wirkung der geschwindigkeitsabhängigen Corioliskraft (blaue Pfeile), die durch die Rotation der Erde verursacht wird. Auf der Südhalbkugel werden alle Bewegungen links abgelenkt.


Anwendung:

Da per Definition Zentrifugalkräfte keine Rolle spielen, ist der geostrophische Wind ein beschleunigungsfreier geradliniger Wind. Er weht daher parallel zu den (nicht gekrümmten) Isohypsen (p-System). Im z-System weht der geostrophische Wind nur quasiparallel zu den Isobaren, da hier das Reziproke der Dichte noch als Proportionalitätsfaktor fungiert. Im Theta-System (mit der potentiellen Temperatur als Höhenskala) weht der geostrophische Wind exakt parallel zu den Isolinien gleichen Montgomery-Potentials. Generell weht der geostrophische Wind umso stärker, je größer der Druck-, Geopotential- oder Montgomery-Potentialgradient ist.

Wie Scale-Analysen zeigen, weicht die geostrophische Approximation nur um durchschnittlich 10% von den realen Winden in der freien Atmosphäre ab. Die Größenordnung der Abweichung des geostrophischen Windes vom Realwind kann mit der sogenannten ROSSBY-Zahl angegeben werden.

Durch seine Einfachheit und gute Genauigkeit, sowohl in Bestimmung als auch in Berechnung, findet er große Anwendung in der Diagnose. Für Prognosen ist der reine geostrophische Wind allerdings unbrauchbar, da Änderungen im Druckfeld von ageostrophischen Windkomponenten ausgehen.
Eine weitere wichtige Bedeutung findet die Geostrophie beim Quasigeostrophischen Konzept. Da der 10%-ge Fehler verkraftbar erscheint, gibt es eine Möglichkeit das vorher nicht geschlossene primitive Gleichungssystem durch die quasigeostrophische Approximation zu schließen. Die dadurch gewonne diagnostische Omegagleichung und die prognostische Geopotentialtendenzgleichung sind das fundamentale Grundgerüst aller numerischen Wettermodelle.



Interpretation des geostrophischen Windes:


Der geostrophische Wind ist eine breitenkreisabhängige Größe, da er von der Corioliskraft abhängt (indirekt proportional zum Coriolisparameter f). In hohen Breiten ist die Corioliskraft größer, so dass hier eine größere Druckgradientkraft zur Aufrechterhaltung des geostrophischen Gleichgewichts von Nöten ist. Im Umkehrschluß bedeutet dies auch, dass in hohen Breiten bei gleichem Druckgradient ein schwächerer geostrophischer Wind weht, als in niedrigeren Breiten.
Die Breitenkreisabhängigkeit zeigt sich auch bei der Berechnung der Divergenz des geostrophischen Windes. Es ergibt sich lediglich ein sphärischer Term, der die Konvergenz der Meridiane in Richtung Pole beschreibt. Daher wird der geostrophische Wind als quasidivergenzfrei bezeichnet. Dies ist anschaulich auch klar, da es sich um einen geradlinigen und beschleunigungsfreien Wind handelt. Da jedoch Änderungen der synoptisch-skaligen Druckgebiete nur über Divergenzen des ageostrophischen Masseflusses stattfinden, wird offensichtlich, dass der geostrophische Wind eine rein diagnostische Größe ist.

In Richtung Äquator wird die geostrophische Approximation natürlich zunehmend schlechter und verliert ihre Gültigkeit. Hier werden andere Approximationen (z.B. EULER-Wind oder zyklostrophischer Wind) angewandt.

© Marcus Boljahn