Idee:

Die Atmosphäre verhält sich nur in der großräumigen synoptischen Skala hydrostatisch. Von entscheidenem Interesse für die Wettervorhersage sind aber oftmals mesoskalige nichthydrostatische Prozesse, vor allem die Feuchtkonvektion. Die vertikalen Schichtungseigenschaften der Atmosphäre geben eine wichtige Auskunft darüber, ob Aufwärtsbewegungen (die ja Feuchtkonvektion auslösen) beschleunigt oder gedämpft werden. Nun ist es aber von essentieller Bedeutung zu wissen, bis zu welchem Höhenniveau und mit welcher Intensität aufwärts gerichtete Vertikalbewegungen stattfinden, denn dies ist ein sehr wichtiges Kriterium bei der Vorhersage mesoskaliger konvektiver Ereignisse, wie z.B. Gewitter. Man also an einer physikalischen Größe interessiert, die umschreibt, wieviel potentielle Energie durch die aktuelle (feuchtlabile) Schichtung bei Feuchtkonvektion in kinetische Energie umgesetzt werden kann. Oder anders formuliert, man sucht ein Maß für die durchschnittliche Labilität der Atmosphäre bei Hebung, welches die Intensität der Vertikalbewegung charakterisiert.


Definition:

Die Labilitätsenergie ist definiert als die Arbeit, die an einem aufsteigendem LAGRANGE`schen Luftpaket zwischen zwei Schichten verrichtet wird. Diese Arbeit ergibt sich aus dem Produkt der ARCHIMEDISCHEN Auftriebskraft und der überwundenen Höhendifferenz. Da die Schichtungskurve in jedem Punkte einen anderen Anstieg aufweisen kann (variierender geometrischer Temperaturgradient), kann demzufolge auch die ARCHIMEDISCHE Auftriebskraft in jedem Niveau einen unterschiedlichen Wert aufweisen, so dass die Labilitätsenergie nur über die Integralbildung sinnvoll ermittelt werden kann.
Analog zur Labilitätsenergie wird oftmals der Begriff CAPE (convective available potential energy) verwendet. Dies ist tatsächliche eine sehr physikalische Beschreibung, denn die Labilitätsenergie gibt letztlich anschaulich an, wieviel potentielle Energie durch Konvektion in kinetische Energie umgewandelt, also verfügbar gemacht, werden kann.
Eine Schichtung in der insgesamt an einem vertikal ausgelenkten Luftpaket keine Arbeit verrichtet wird, oder gar dieses Luftpaket Arbeit verrichten muss um eine Vertikalbewegung auszuführen, wird mit CAPE=0 definiert. Ist CAPE positiv, so spricht man von einer latent labilen Schichtung.
Da jedoch Feuchtkonvektion nicht immer zwingend vom Boden ausgehen muss, werden sinnvollerweise weitere "Unterarten" von CAPE definiert, die jeweils eine untere Grenze der Integration besitzen.
SBCAPE (surface based CAPE) beschreibt die gesamte atmosphärische Labilitätsenergie eines direkt vom Bodenniveau aus gehobenen Luftpakets. Alle von der Grundschicht abgekoppelten konvektiven Ereignisse (abgehobene "elevated" Konvektion) werden mit dieser Methode zumeist stark unterschätzt. Auch eine Überschätzung der konvektiv möglichen Tätigkeit ist bei SBCAPE möglich, wenn nämlich der bodennahe Taupunkt in einer insgesamt aber eher trockenen PGS extrem hoch ist.
MUCAPE (most unstable CAPE) ist dagegen der höchste CAPE-Wert in der Tropopause und wird daher erst vom LFC aus berechnet. Im Extremfall ist MUCAPE=SBCAPE, wenn das LFC genau im Ausgangsniveau sich befindet. Mit Hilfe von MUCAPE kann man vor allem die Möglichkeit einer abgehobenen Konvektion besser beurteilen.
MLCAPE (mixed layer CAPE) wird analog dem SBCAPE auch vom Boden aus aufintegriert, allerdings werden als Ausgangsdaten die mittleren Temperatur- und Feuchtewerte der unteren 100 hPa als Startwert für die Hebungskurve zur Berechnung von MLCAPE verwendet. Um dem beim SBCAPE erwähnten Fehler bei starkem vertikalen Taupunktsgradient entgegenzuwirken, wird MLCAPE berechnet. Gelegentlich wird auch nur über die untersten 50 oder 30 hPa gemittelt. Man erwähnt dies dann explizit dahinter als MLCAPE50 oder MLCAPE30.
Allen gemeinsam ist die gleiche definierte Integrationsgrenze. Dies ist das sogenannte Gleichgewichtsniveau (equillibrium level), welches den letzten Schnittpunkt von Hebungs- und Schichtungskurve darstellt. Allerdings hat die Hebungskurve jeweils andere Startpunkte, so dass das Gleichgewichtsniveau bei den verschiedenen CAPE-Arten im Normalfall unterschiedlich hoch liegt. Je nach vertikaler Schichtung liegt dieses Gleichgewichtsniveau zwar meistens in der Nähe der Tropopause, kann sich aber sowohl darüber als auch darunter befinden.


Anschauung:

Verwendet man in einem Temp als Ordinate ln p, so ergibt sich CAPE sehr anschaulich aus der Schnittfläche zwischen Hebungskurve und Schichtungskurve, denn die umschlossenen Flächen der Zustandskurven in solchen Diagrammen sind proportional zur verrichteten Arbeit. Dabei entstehen die gewünschten positiven CAPE-Werte wenn die Hebungskurve im Vergleich zur Schichtungskurve auf der (wärmeren) rechten Seite liegt. Nun gibt eine einfache graphische Addition der Flächen darüber Aufschluß, ob eine latent labile Schichtung (CAPE positiv) vorliegt und vertikale Bewegungen durch die Schichtung beschleunigt werden.


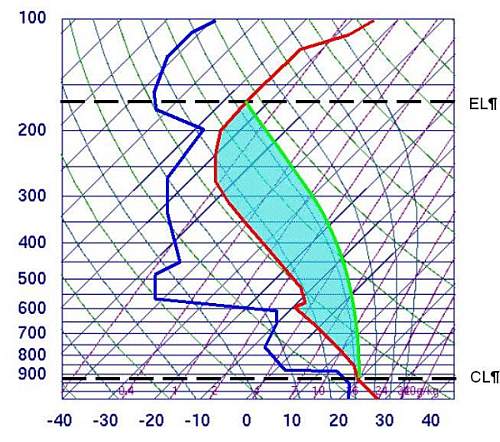
Quelle: www.wetteran.de

Die unterste Grenzschicht ist bis zum LFC trockenindifferent geschichtet, so dass Hebungs- und Schichtungskurve exakt gleich verlaufen. Ab dem LFC folgt die Hebungskurve der Feuchtisentropen bis sich beide Kurven im Gleichgewichtsniveau (EL) letztmalig schneiden. Die türkise Fläche repräsentiert also SBCAPE, der in diesem Fall nahezu exakt mit MLCAPE wäre.



Quelle: www.wetteran.de

Diese Abbildung zeigt sehr anschaulich den Unterschied zwischen SBCAPE und MUCAPE. Während SBCAPE (grüne gestrichelte Linie) Null ist, ergibt sich für die ab dem LFC berechnete MUCAPE positive Werte. Somit besteht die Möglichkeit für abgehobene "elevated" Konvektion, falls die unterste feuchtstabile Schicht mit Vertikalbewegung überwunden werden kann.


Anmerkung: Das oftmals benutzte STÜVE-Digramm benutzt als Ordinate p hoch kappa, so dass CAPE hier nicht mehr proportional zur eingeschlossen Fläche zwischen Hebungs- und Schichtungskurve ist. Dafür ergeben sich in dieser Diagrammform geradlinig ansteigende Isentropen, so das die potentielle Temperatur leichter bestimmt werden kann.

Allgemeine Erklärung und Interpretation der atmosphärischen Schichtungseigenschaften unter: vertikale Stabiltätsmaße

© Marcus Boljahn