Glossar

Idee:

Beim Versuch eine allgemeine Berechnungsgrundlage für die Strömungsgeschwindigkeit in der Höhe aufzustellen, kam C.G. ROSSBY 1939 unter einigen vereinfachenden Annahmen zu dem Ergebnis, dass lediglich eine periodische Wellenlösung für die aus Vorticity- und Kontinuitätsgleichung gewonnene harmonische Differentialgleichung 2.Ordnung in Frage kommt. Damit war die Existenz und vor allem die Verlagerung atmosphärischer Wellen rechnerisch nachgewiesen, die bis dato durch das eher bescheidene Messnetz nur vermutet worden waren. Er konnte ferner auch eine Formel für die Phasengeschwindigkeit dieser als ROSSBY-Wellen bezeichneten atmosphärischen Wellen angeben.

Definition:

ROSSBY-Wellen sind horizontal-transversale atmosphärische Wellen, welche in einem reibungsfreien und inkompressiblen Medium bei rein horizontalen scherungsfreien Strömungen den stabilen Grundzustand bilden.

Anschauung:

ROSSBY machte, wie in der Definition erkennbar, vier wichtige Annahmen. Zuerst ging er von einer rein horizontalen Bewegung aus, um Schwerewellen herauszufiltern, die bekanntlich vertikal-transversale Wellen sind. Zudem sollte diese Bewegung in y-Richtung keine Scherung aufweisen, so dass für ein Luftteilchen sich die Bewegung auf eine eindimensionale Bewegung entlang einer Trajektorie vereinfacht. Drittens traf er die Approxmation einer komplett reibungsfreien Atmosphäre, was in der freien Atmosphäre tatsächlich sehr gut realisiert ist. Zu guter letzt soll es sich um ein inkompressibles Medium handeln, um auch Schallwellen herauszufiltern. Daher stellt die Dichte eine Konstante dar, was im Umkehrschluss über die Kontinuitätsgleichung bedeutet, dass die Strömung divergenzfrei verläuft. Analog ist durch die konstante Dichte auch die Barotropiebedingung erfüllt.
Diese letzte Annahme berechtigt nun auch zur Verwendung der divergenzfreien barotropen Vorticitygleichung, nach der die absolute Vorticity eine Erhaltungsgröße darstellt. Anschaulich bedeutet dies, dass bei polwärtigen meridionalen Strömungen zyklonale Vorticity auf Kosten steigender Erdvorticity abgebaut wird und umgekehrt bei meridionalen Strömungen in Richtung Äquator die antizyklonale Vorticity (bei abnehmender Erdvorticity) ansteigt. Demnach stellt die breitenkreisabhängige Erdvorticity den rücktreibenden Antrieb für die ROSSBY-Wellen dar, denn eine polwärtige Strömung erhält durch die größer werdender zyklonaler Vorticity natürlich auch eine zyklonale Krümmung, welche in Bewegung zurück in Richtung Äquator auslöst. Umgekehrt wird eine zum Äquator gerichtete Strömung durch die größer werdende antizyklonale Vorticity auch zunehmend antizyklonaler gekrümmt und kehrt quasi um. Der beschriebene Vorgang wird oftmals auch als Beta-Effekt bezeichnet.

Phasengeschwindigkeit:

Die Phasengeschwindigkeit (C) ist nun abhängig vom mittleren zonalen Grundstrom (U) sowie der meridionalen Variation der Erdvorticity (ß) und dem Quadrat der Wellenlänge (L²). Sie beschreibt die Geschwindigkeit der stromabwärtigen (progressiven) Ostwärtsverlagerung einer ROSSBY-Welle. Stromaufwärtige (retrograde) Verlagerungen sind durch negative Phasengeschwindigkeiten gekennzeichnet. Ist C=0, so erfolgt keine Verlagerung und man spricht von einer stationären ROSSBY-Welle.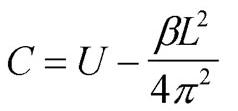



Aus der ROSSBY-Formel sofort ersichtlich wird die Tatsache, dass sich ROSSBY-Wellen immer langsamer als die mittlere zonale Grundstromgeschwindigkeit verlagern können, da sowohl U als auch ßL² positive Terme ergeben. Dabei ist die Phasengeschwindigkeit umso höher, je kleiner die Wellenlänge ist. Die Abhängigkeit der Phasengeschwindigkeit von der Wellenlänge bezeichnet man als Dispersion. Die diese Abhängigkeit quadratischer Natur ist, erhöht sich die Phasengeschwindigkeit für besonders kurze Wellen dann auch recht schnell. Bei besonders langen Wellen kann der zweite Term in Einzelfällen auch negativ werden, so dass sich hier eine retrograde Westverlagerung der ROSSBY-Welle ergibt. Sind beide Terme auf der rechten Seite identisch, so folgt eine stationäre Welle.
Natürlich ist die Phasengeschwindigkeit (über ß) auch von der geographischen Breite abhängig. Dies lässt sich besonders anschaulich im Fall der stationären ROSSBY-Wellen (C=0) zeigen. In den hohen Breiten (60-70°N) bei kleinem ß (die Erdvorticity ist hier zwar groß, aber die meridionale Zunahme ß ist dagegen recht klein) werden nur sehr lange Wellen (Wellenzahlen 2, 3) stationär. Dagegen können in den niedrigeren Breiten (30-40°N) bei großem ß auch kürzere Wellen (Wellenzahlen 5, 6, 7) schon stationär werden. Die Wellenzahl selbst gibt die Anzahl der hemisphärischen Tröge bzw. Keile an und ist dementsprechend umgekehrt proportional zur Wellenlänge.


Entstehungsprozess: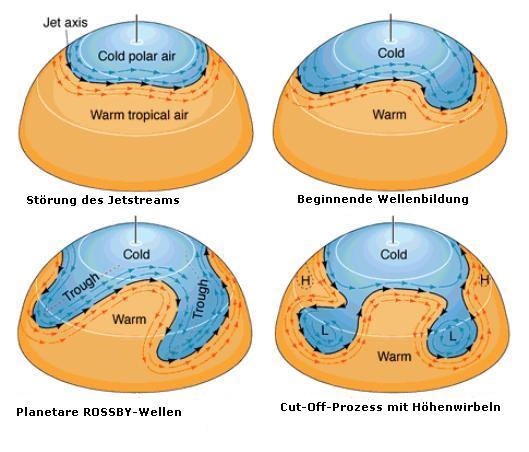



Diese Skizze beschreibt in vier Schritten sehr anschaulich die Entstehung planetaren ROSSBY-Wellen bis hin zum Cut-Off-Prozess und der Bildung von Höhenwirbeln. Eine in den Jetstream eingelagerte Störung bildet den Anfangspunkt einer Wellenbildung. Infolge barokliner Instabilität (Diese hat ROSSBY ironischerweise bei seinen Annahmen zwar ausgeschlossen, aber dennoch ist sie tatsächlich ursächlich für die Ausweitung der Keile und Tröge. ROSSBY beschrieb mit seiner Ausarbeitung auch nicht den Entstehungsmechanismus, sondern erklärte lediglich Verlagerung von planetaren Wellen. Streng nach ROSSBY bleiben also einmal bestehende Wellen in immer fortwährender Stärke bestehen und verlagern sich lediglich.) können sich nun die Keile und Tröge weiter amplifizieren, was auch in der Diskussion der Geopotentialtendenzgleichung herausgestellt wurde. Im dritten Schritt erreichen die ROSSBY-Wellen den Höhepunkt ihrer Entwicklung. Übertrifft die Amplitude die Wellenlänge, so werden die planetaren Wellen in der Regel sehr instabil und eine abschnürender Cut-Off-Prozess wird eingeleitet.


Anwendung:

Trotz der recht scharfen Annahmen, erweist sich die Approximation von ROSSBY insbesondere für die Wellenzahlen 4-9 als sehr realitätsnah. Die stationären Wellen 1-3 werden eher durch die relative Lage der Kontinente, insbesondere der Gebirge sowie durch die Land-Meer-Verteilung bestimmt, so dass hier die ROSSBY-Formel keine guten Werte liefert. Auch kürzerwellige barokline Phänomene werden durch die rein barotrope Betrachtungsweise von ROSSBY nicht mehr gut erfasst. Dennoch liefert diese Vorgehensweise erstaunlich gute Ergebnisse, was ROSSBY aber auch einer kompensierenden Wirkung zweier weiterer wichtiger Aspekte verdankt.
Zum einen werden in Richtung der Pole durch die Kugelgestalt der Erde die Stromlinien richtungskonvergent. Dadurch entsteht ein kanalisierender, also beschleunigender Effekt, den HAURWITZ untersucht hat. HAURWITZ-Wellen sind somit stets schneller als ROSSBY-Wellen.
Auf der anderen Seite hatte ROSSBY divergenzfreie Strömungen betrachtet, was natürlich auch nur in grober Näherung stimmt. Einerseits erfolgt wie bereits oben beschrieben ein richtungskonvergenter sphärischer Effekt, aber andererseits tritt vor allem bei kurzen Wellen eine Richtungsdivergenz durch die Änderung der Krümmung entlang einer Welle auf, so dass dadurch ein Abbremsen der ROSSBY-Welle verursacht wird.
Das gleichzeitig wirksame Beschleunigen durch den Kanalisierungseffekt und Abbremsen durch den Divergenzeffekt wurde zwar durch ROSSBY nicht berücksichtigt, durch die kompensatorische Wirkung entsprachen seine Ergebnisse aber dennoch sehr gut den realen Beobachtungen.


Stabilität barokliner planetarer Wellen:

Die ROSSBY-Welle, selbst mit all den getroffenen Annahmen, stellt einen stabilen Grundzustand in der barotropen Atmosphäre dar. Wie beim Entstehungsmechanismus bereits erwähnt, ist jedoch Baroklinität ein notwendiges Kriterium um planetare Wellen zu bilden. In diesem Zusammenhang ist es sinnvoll die Stabilität barokliner planetarer Wellen zu untersuchen. Dies kann man am einfachsten anhand eines Amplitudenvergleichs zwischen Temperatur- und Strömungswelle realisieren.
Der triviale Fall eines reinen wellenförmigen Isohypsenfeldes beschreibt den stabilen barotropen Fall der ROSSBY-Wellen. Nun lassen sich aber darüberhinaus auch drei verschiedene barokline Fälle diskutieren, wo der Einfachheit halber ein konstanter meridionaler Temperaturgradient angenommen wird.
Im ersten Fall sind Isothermen- und Isohypsenwelle in Phase, was einer stabilen planetaren Welle entspricht, dessen Verlagerung vom Vergleich der Amplituden abhängt. Bei einer größeren Temperaturwellenamplitude verlagert sich die stabile Welle langsam progressiv stromabwärts. Umgekehrt kommt es zu einer retrograden stromaufwärtigen Wellenverlagerung, wenn die Isohypsenamplitude größer ist. Im äquivalent barotropen Fall identischer sich in Phase befindlicher Amplituden bildet sich eine stationäre Welle aus.
Auch der zweite Fall einer inversen Phase beschreibt stabile planetare Wellen. Allerdings kommt es in diesem wenig realistischen Fall zu einer sehr raschen progressiven Verlagerung.
Erst im dritten Fall einer um ca. 90° nach hinten phasenverschobenen Temperaturwelle beschreiben planetare Wellen einen instabilen Zustand. Solche baroklinen Wellen verlagern sich meist rasch progressiv und sind mit Zyklogenese verbunden.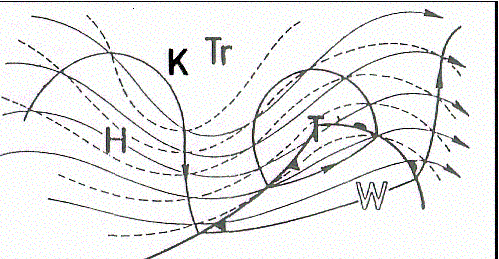



Auf der Skizze ist sehr schön die gegenüber der Isohypsenwelle stromaufwärts phasenverschobene Temperaturwelle zu erkennen. Auf der Trogvorderseite kommt es nun zur Advektion thermischer Vorticity und damit zu Vertikalbewegung.


Besondere atmosphärische Welleneigenschaften und Energetik:

Die Atmosphäre realisiert nur in den seltensten Fällen ganzzahlige Wellenregime. Stattdessen ist die nordhemisphärische Zirkulation ein Ergebnis aus zahlreichen Überlagerungen verschiedenster planetarer Wellen. Solch eine räumliche Anordnung und Überlagerung verschiedenster Wellen wird auch als Wellenpaket bezeichnet. Wellenpakete umschreiben somit quasi die räumliche Konzentration der Wellenenergie. Die Verlagerung von Wellenpaketen geschieht dabei mit der sogenannten Gruppengeschwindigkeit, die bei planetaren Wellen allgemein größer ist, als die Geschwindigkeit des mittleren zonalen Grundstroms und damit auch über der Phasengeschwindigkeit liegt. Diese erstaunliche Eigenschaft bezeichnet man als anomal dispersiv, wobei die grundsätzliche dispersive Eigenschaft der planetaren Wellen bereits an der ROSSBY-Formel gezeigt wurde.
In der Praxis ist diese anomale Dispersion bei den energiereichen kurzen Wellen zu beobachten. So durchläuft ein Kurzwellentrog unter Verstärkung (und mit ihm auch das betrachtete Wellenpaket) den übergeordneten Langwellentrog weitaus rascher, als dieser sich mit seiner Phasengeschwindigkeit verlagern kann. Ist der Kurzwellentrog in einen Langwellenkeil eingelagert, so durchläuft er diesen zwar auch recht schnell, allerdings unter Abschwächung. Die jeweils umgekehrten energetischen Prozesse sind bei Kurzwellenkeilen zu beobachten, die unter Verstärkung einen Langwellenkeil und unter Abschwächung einen Langwellentrog durchlaufen.


© Marcus Boljahn

 back to top

copyright by www.diplomet.info