Defintion:

Der thermische Wind ist definiert als der geostrophische Differenzwind zwischen zwei Höhenniveaus.

Anschauung:

Die Berechnung des thermischen Windes ist anschaulich durch die Differenzbildung recht einfach, wie auch die folgende Skizze des thermischen Windes zwischen 850 hPa und 500 hPa zeigt.


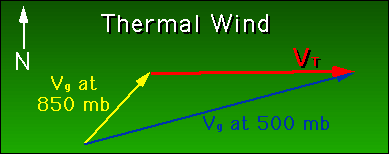
Oftmals von Interesse ist aber der differentielle thermische Wind. Dieser beschreibt die Änderung des geostrophischen Windes mit der Höhe. Anschaulich ergibt sich bei der Berechnung nun ein Wind, der im p-System exakt parallel zu den Isothermen "weht". Er ist umso stärker, je größer der Temperaturgradient und je kleiner der Coriolisparameter ist. Auf der Nordhemisphäre liegt die wärmere Luft auf der rechten Seite. Daher ergibt sich im Mittel ein westlicher thermischer Wind. Im z-System sorgt die Dichteabhängikeit noch für einen kleinen Zusatzterm, so dass der (differentielle) thermische Wind nur quasiparallel zu den Isothermen "weht". Der (differentielle) thermische Wind ist natürlich kein real existierender Wind, daher die Anführungszeichen, jedoch können mit seiner Hilfe sehr wertvolle Aussagen unter anderem über Temperaturadvektion und Baroklinität gewonnen werden.


Bedeutung:

Die Existenz eines isobaren Temperaturgradienten induziert per Definition einen thermischen Wind. Gleichzeitig ist dies aber auch ein notwendiges Baroklinitätskriterium. Dementsprechend kann man allein aus der Existenz eines thermischen Windes auf eine barokline Atmosphäre schließen. Umgekehrt lässt sich anhand des quasihorizontalen Temperaturgradienten (auf einer p-Fläche) über die thermische Windbeziehung nun auf die allgemeine Windverteilung schließen. Da der Bodenwind infolge der Reibung allgemein als gering angesehen werden kann, gibt die Temperaturverteilung einen direkten Hinweis auf die Windverteilung in der jeweils betrachteten Höhe.
Gibt es eine richtungsändernde Komponente der geostrophischen Windänderung, so verursacht der resultierende thermische Wind eine Temperaturadvektion. Erfolgt von Boden aus gesehen eine antizyklonale geostrophische Winddrehung (Rechtsdrehung auf Nordhemisphäre) mit der Höhe, so erfolgt Warmluftadvektion. Umgekehrt deutet eine zyklonale Winddrehung (Linksdrehung) auf Kaltluftadvektion.



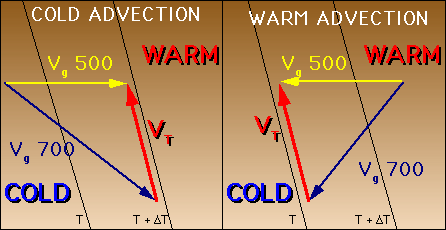
Die Skizze verdeutlicht diese Drehung des geostrophischen Windes sehr anschaulich. Links die KLA bei mit der Höhe (von 700 hPa auf 500 hPa) linksdrehendem Wind. Auf dem rechten Bild der umgekehrte Fall eine WLA.

Ändert der geostrophische Wind mit der Höhe nur seine Geschwindigkeit aber nicht seine Richtung, so ist die Atmosphäre zwar barokliner Natur, aber es erfolgen keinerlei Temperaturadvektionen. Man spricht in diesem Fall daher auch von einer äquivalent barotropen Situation.


Weitere Anwendung:

Eine neue praktische Anwendung des thermischen Windes fand TRENBERTH 1970 in seiner Formulierung der diagnostischen Omegagleichung. Er zeigte, dass Vertikalbewegungen direkt proportional zur Advektion der absoluten geostrophischen Vorticity durch den thermischen Wind sind. Damit reicht allein die Kenntnis des thermischen Windfeldes und des Vorticityfeldes aus, um Vertikalbewegungen zu diagnostizieren. Somit entfällt ein entscheidender Nachteil der Omegagleichung, denn es kommen keine kompensierende Terme mehr vor.
In der PGS induziert das untere inhomogene Dichtefeld natürlich auch ein thermisches Windfeld. Dabei zeigt sich, dass der thermische Wind in der PGS oftmals eine kompensatorische Wirkung hat. So "weht" der thermische Wind beispielsweise antizyklonal um einen Warmluftsektor. Als Konsequenz ergibt sich auf der warmen Seite der Frontalzone am Boden eine Konvergenzlinie.


© Marcus Boljahn